Implementation
To improve the pathfinding effiency I implemented a modified version of the hexx crate. Instead of taking into account the entire hexagon grid as a graph to find the shortest path, you subdivide the whole grid in a hierachy of sub-grids. Every subgrid has all entrences to all it’s neighbour sub-grids identified. You define entrences for every continious tile that is open on both neighbouring sub-grid. If you find a long continous line of open tiles, you can put an entrence on the edges of the line. If it’s only a few open tiles, you put an entrence in the middle.
Check the beyondastar.pdf in resources for a visible example.
For every sub-grid you do the normal A* pathfinding for only that sub-grid from every entrence to every entrence. You only store the weight of the edge between the entrence. That leaves you with a weighted graph that’s a lot more efficient to calculate a path. You also calculate the path from the start and end to every entrence in the sub-grid they are located in.
The result is faster, but a less optimal pathfinding algorithm. Especially as you only define the graph one time during initialization.
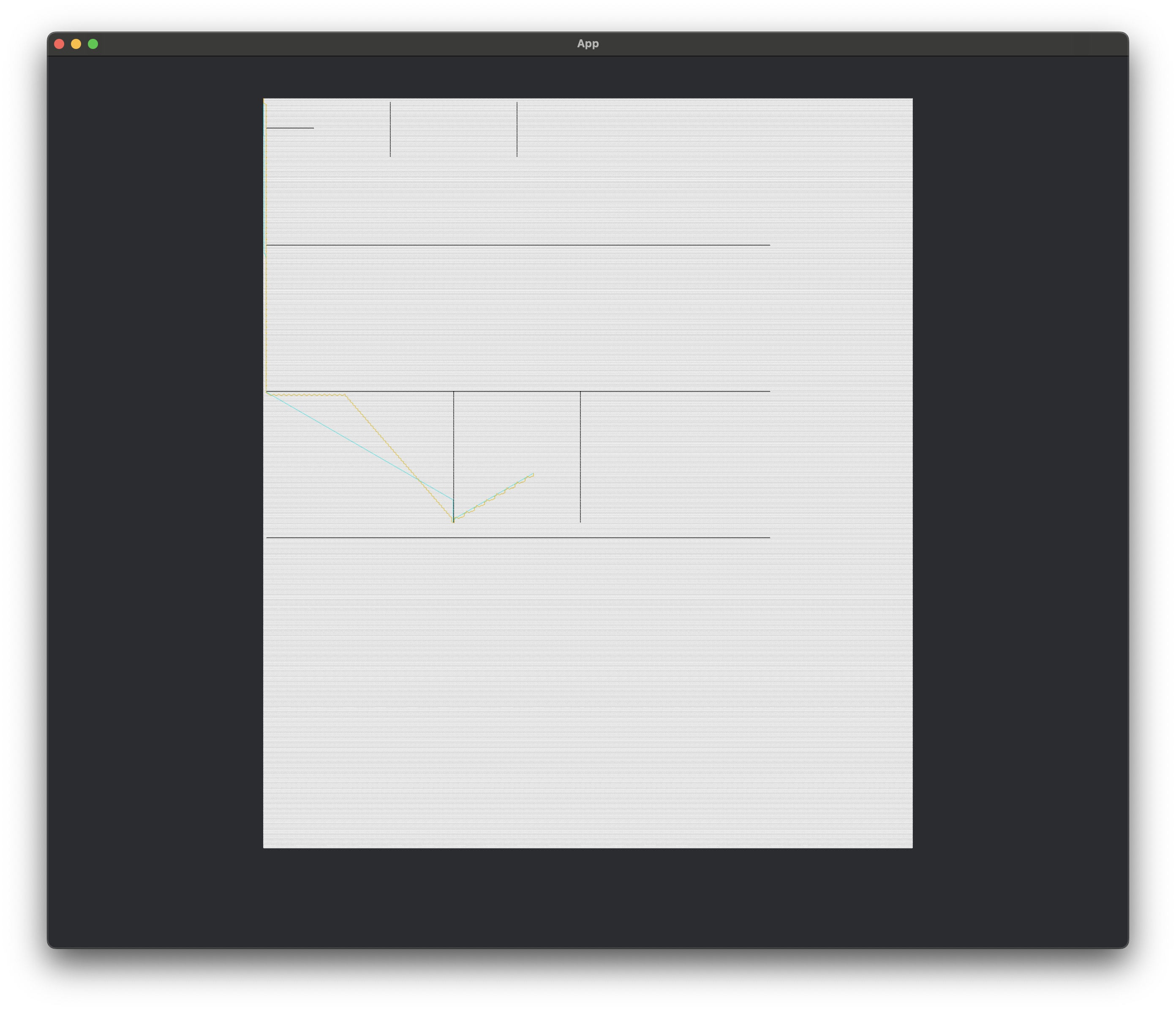
In the picture the blue line is by normal A* pathfinding algorithm on a 1024 * 1024 hexagon grid. The gold line is the hierarchical implementation on the same grid. The white tiles are open, and the black tiles are closed (don’t allow movement.)
Blue line took 314.6105ms, to calculate the route and was 912 tiles long.
Gold line took only 15.133ms to calculate, but was 1016 tiles long.
This means trading a 20x speed gain for approximately a 10% reduction in precision.
Resources
- https://gamedev.stackexchange.com/questions/151456/haa-hpa-c-algorithm-help
- https://gamedev.stackexchange.com/questions/192183/how-does-hpahierarchical-pathfinding-a-really-work/192186#192186
- https://web.archive.org/web/20190411040123/http://aigamedev.com/open/article/clearance-based-pathfinding/
- https://harablog.wordpress.com/wp-content/uploads/2009/06/beyondastar.pdf